C A L C U L A T O R

As I have mentioned in my earlier post, a calculator is required to solve trigonometric problems. 

Where the sine, cosine and tangent key can be found is shown below. 

To access the inverse sine, cosine or tangent key, press shift + the sine, cosine or tangent key.

- k.v.

IN REAL L I F E

Trigonometry is actually quite relevant especially relating to real life situations. We often, however fail to foresee its importance as we refrain from thinking about its relevance.

Trigonometry is required in many career paths such as:

- architecture
- biology
- chemistry
- actuary
- animation
- astronomy
- attorney

and many more.

Trigonometry is commonly used in finding the height of towers and mountains.




It is used in finding the distance between celestial bodies.



The sine and cosine functions are fundamental to the theory of periodic functions such as those that describe sound and light waves.



Trigonometric identities are found heavily in architecture. especially when developing large infrastructure. The six different identities are used to find either the length of one one or more sides of a shape, or the angle at which different materials should be placed at. It is common to find them when constructing blueprints for actual structures. (Examples of this are shown below.) 




Trigonometric identities are applicable in the field of music for stringed instruments.  For example, the vibration of a violin possesses the same shape as a sine function. When playing instruments you don't think about trigonometric identities, but when calculating the physics behind it, they come into play. Trig identities in music are typically a calculation of frequency and are represented by using kilohertz (kHz) 

- k.v.

T H E U N K N O W N

In order to find the unknown side or angle you must have a scientific calculator. Ensure that your scientific calculator is in degree mode.
To find the unknown side:

We first decide which of the trigonometric ratios must be used; In this problem we must use the sinθ ratio since the opposite side (O) and the hypotenuse (H) are involved.

We then multiply both sides by 41 and evaluate using the calculator.



sin 25° = x / 41

 x = 41 sin 25° 
      
    =17.33           





To find the unknown angle:

Just like finding out the unknown side we must first decide which of the trigonometric must be used; In this problem we must use the tanθ ratio since the opposite side (O) and the adjacent side (A) are given.

We then use the inverse tangent key on your calculator 

  
    
      tan θ = 16/22
       
      θ = 36.027.....°
      
      θ = 36°

- k.v.

B E A R I N G S

Bearings are used to indicate direction and therefore are commonly used to navigate the sea or air in ships or planes. Bush walkers use bearings with a compass to help follow a map and navigate a forest. The most common type of bearing is the true bearing measured clockwise from north.

- k.v.

P Y T H A G O R A S

Pythagoras was born on the Greek island of Samos in the 6th century BC. He received a privileged education and traveled to Egypt and Persia where he developed his ideas in mathematics and philosophy. He settled in Crotone, Italy, where he founded a school. His many students and followers were called the Pythagoreans and under the guidance of Pythagoras, lived a very structured life with strict rules. 

The Pythagoreans discovered the famous theorem, which is named after Pythagoras, and the existence of irrational numbers, which cannot be written down as a fraction or a terminating decimal. Such numbers cannot be measured exactly with a ruler with fractional parts and were thought to be unnatural. The Pythagorans called these numbers 'unutterable' numbers and it is believed that any member of the brotherhood who mentioned these numbers in public would be put to death.

- k.v.

E L E V A T I O N & D E P R E S S I O N

Angles of elevation or inclination are angles above the horizontal, like looking up from ground level toward the top of a flagpole. If the object is below you, the angle of depression is the angle your eyes look down.

Angles of depression or declination are angles below the horizontal, like looking down from your window to the base of the building in the next lot. 
















Whenever you have one of these angles, you should immediately start picturing how a right triangle will fit into the description.

Angles of elevation and depression are measured from the horizontal. It is common mistake not to measure the angle of depression from the horizontal.

Using the angle of depression or elevation to an object, and knowing how far away the object is, enables us to find the height of the object using trigonometry.

The advantage of doing this is that it is very difficult to measure the height of a mountain or the depth of a canyon directly; it is much easier to measure how far away it is (horizontal distance) and to measure the angle of elevation or depression.

Suppose that we want to find the height of this tree. We mark point A and measure how far it is from the base of the tree and then we measure the angle of elevation from A to the top of the tree.















Now,






we have measured x and θ, so we can calculate tanθ and thus we can find h, which is the height of the tree.

-k. v.

R I G H T - A N G L E D T R I A N G L E S

As right-angled triangles are a key area of study in trigonometry I felt that it would be rather necessary to make a post purely based on right-angled triangles.

The right-angled triangle is one of the most useful shapes in all of mathematics. It is used in the Pythagoras Theorem and Sine, Cosine and Tangent.

A right-angled triangle is simply a triangle that has a right angle (90°) in it. Every right-angled triangle has a little square in the corner which indicates  that it is in fact a right-angled triangle.

In a right-angled triangle the three sides are given special names. The side opposite the right angle is called the hypotenuse which is always the longest side of the triangle. The other two sides are named in relation to another known angle (or an unknown angle under consideration). 

If this angle is known or under consideration then the side opposite from it is called the opposite side because it is opposite the angle and the side next to it is called the adjacent side because it is adjacent to  the angle.

- k.v.

P Y T H A G O R A S' T H E O R E M

Over 2000 years ago there was an amazing discovery made by the Pythagoreans and this was: when the triangle has a right angle (90°)  and squares are made on each of the three sides, then the biggest square has the exact same area as the other two squares put together. It is called "Pythagoras' Theorem". Pythagoras' theorem states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

Pythagoras:

- k.v.

T R I G O N O M E T R Y

    

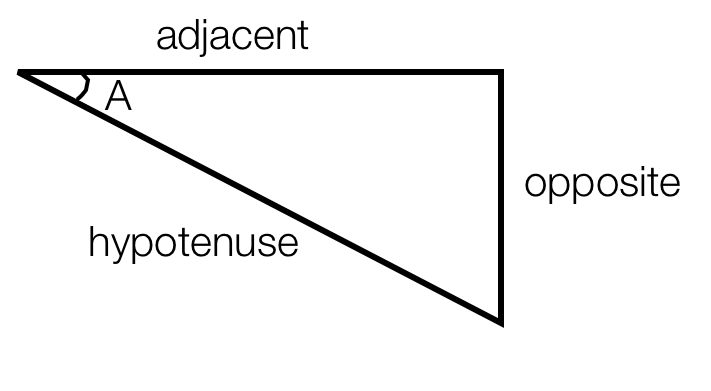
As you can see, the word itself refers to three angles - a reference to triangles.

The word 'trigonometry' is commonly believed to originate from the Greek words trigonon and metron which mean "triangle" and "measure". Trigonometry is literally the measuring (of angles and sides) of triangles.This is a very old science that may have been used in a basic form in ancient Egypt. It was the Greeks that formalized the first trigonometric functions, starting with Hipparchus of Bithynia in around 150 B.C.

Trigonometry is a specialist branch of geometry that deals with the study of triangles. It is sometimes informally referred to as "trig." In trigonometry, we study the relationships between the sides and angles of triangles. Right triangles are a key area of study in this area of mathematics.

Trigonometric functions describe the relationships between the angles and sides of a triangle. In modern, mathematics, there are six main trigonometric functions, also called trigonometric formulas: sine, tangent, secant, cosine, cotangent, and cosecant. These functions describe the ratios of the sides of right triangles.

Trigonometric identities are algebraic equations that are important elements of the study of triangles. Trigonometric identities include Pythagorean identities, reduction formulas, and cofunction identities. Often, a trigonometry calculator is used to solve trig problems.

Trigonometry courses may cover study topics such as how to use the trigonometric functions to solve right triangles, and the Pythagoras' Theorem. In addition, non-right angled triangles can be solved using the sine and cosine trigonometric functions. More advanced educational courses may include the study of complex numbers, polar coordinates, De Moivre's Theorem, and Euler's Formula. 

- k.v.

S O H C A H T O A

There are three main functions in trigonometry and they are sine (sin), cosine (cos) and tangent (tan). These three main functions help us find a missing side or angle. Sine, cosine and tangent are all based on a right-angled triangle. 

For a right-angled triangle with a given angle θ, the three main functions sine, cosine and tangent are given by:

sine of an angle θ = Opposite / Hypotenuse

cosine of an angle θ = Adjacent / Hypotenuse

tangent of an angle θ = Opposite / Adjacent

SOHCAHTOA is a useful way of remembering the three main functions.

- k.v.